国家天元数学西北中心定于6月21日至6月29日在腾讯会议室线上举办“孤立子和可积系统前沿理论讲习班”的第三期活动。该讲习班是西北中心2022年促进西部地区发展活动之一，主要为从事相关研究的青年教师及在校研究生系统性讲授孤立子和可积系统理论中的一些基本理论和核心方法，促进西北及周边地区教师人才在基础数学方面研究质量的提升。本次讲习班第三期活动的课程内容主要涉及可积系统的Riemann-Hilbert 方法，包括七次课程（每次两个小时）和三个前沿学术讲座。

【日程安排】

时间：6月21日-6月29日

地点：腾讯会议612-5229-1974

密码：202206

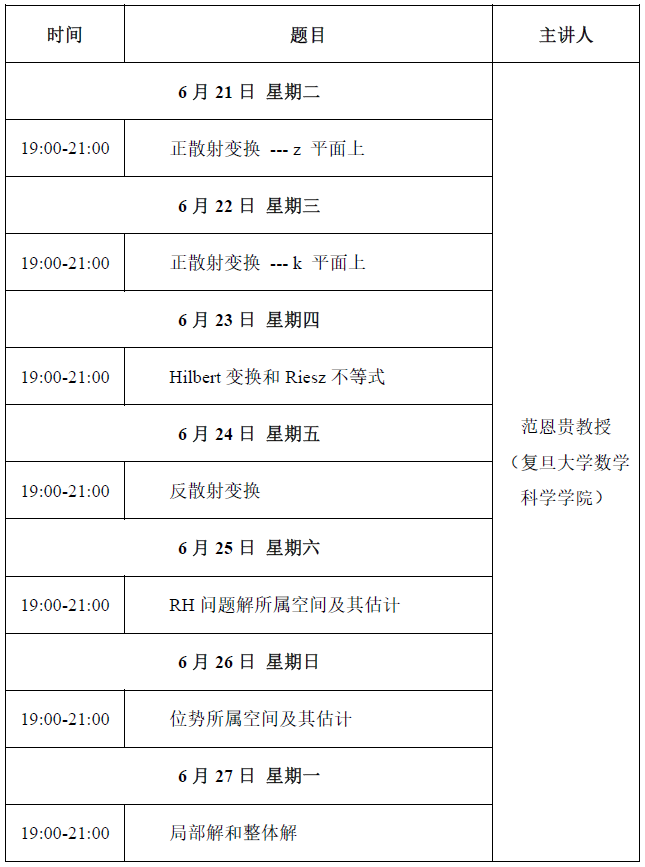
【课程简介】

Riemann-Hilbert (RH) 问题是著名数学家Hilbert在国际数学家大会所提出的23个著名数学问题中的第21个问题，对二十世纪数学发展产生了深远的影响。1908年, Plemelj对RH问题做出了肯定回答；1989年，Bolibruch关于RH问题举出反例；20世纪70年代，ICM报告者Zakharov等学者首先将可积系统与RH问题联系起来。目前，已被发展成为解决一大类纯粹和应用数学相关问题强有力的分析工具---RH方法，成功地应用于可积系统、zero-dispersion 极限问题、Toda格的shock、量子场和统计力学模型、无穷维Grassmann流形、正交多项式、随机矩阵理论等，形成了近十年国际上纯粹数学和应用数学的研究热点。

   在本期系列课程中，我们将以导数Schrödinger方程为例，系统讲授利用反散射变换理论和RH方法建立加权Sobolev初值下可积系统整体解存在性的基本思想和方法。Jost函数和散射数据关于初值的Lipschitz连续性、位势关于反射系数的Lipschitz连续性、Fredholm算子方程、Cauchy投影算子等在这种方法中起关键作用。与经典的偏微分方程理论相比，这种方法的优势在于无需对初值做小范数假设。

主讲人简介

   范恩贵，复旦大学数学科学学院教授，博士生导师，上海市曙光学者。主要从事可积系统、正交多项式和随机矩阵方面的研究。在Adv. Math.、SIAM J. Math. Anal.、J. Differential Equations等国际重要期刊发表论文100余篇。应邀访问美国密苏里大学、密歇根州立大学、日本京都大学等。曾获得教育部自然科学二等奖、上海市自然科学二等奖和谷超豪数学奖等多个奖项。

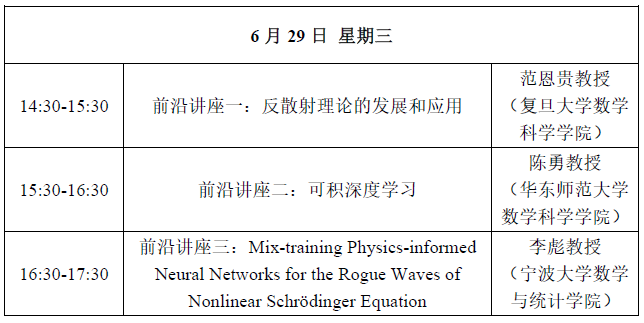
【前沿讲座一】

题目：反散射理论的发展和应用

摘要：1967年，Gardner、Greene、Kruskal和Miura 发现求解KdV方程快速衰减初值问题的反散射方法，该方法是Fourier变换在非线性可积偏微分方程中的自然推广。反散射方法的产生被认为是可积系统发展的里程碑性工作。本报告将详细综述反散射理论的产生和发展，特别分析其中经典反散射方法、Riemann-Hilbert方法和Dbar方法的关键思想和步骤。虽然反散射理论产生有50年历史，但仍然有大量公开问题没有解决，这里我们引述美国科学院院士Deift提出的二个公开问题。

报告人：范恩贵，复旦大学数学科学学院教授

【前沿讲座二】

题目：可积深度学习

摘要：介绍非线性科学与计算机发展关系-可积系统，探讨我们提出的可积深度学习的理论架构和发展方向。介绍我们有关可积深度学习的研究工作：基于PINN算法并对其改进，研究可积方程中的多孤子，高阶呼吸子，高阶怪波，周期背景下的高阶怪波，向量多孤子，孤子分子及其动力学行为；提出了高维可积系统PINN算法；提出了基于守恒律的两阶段PINN算法的提出。

报告人简介

陈勇，华东师范大学数学科学学院教授，博士生导师， 计算机理论所所长，上海市闵行区拔尖人才。长期从事非线性数学物理、可积系统、计算机代数及程序开发、可积深度学习算法、混沌理论、大气和海洋动力学等领域的研究工作。提出了一系列可以机械化实现非线性方程求解的方法，发展了李群理论并成功应用于大气海洋物理模型的研究。提出可积深度学习算法，开发出一系列可机械化实现的非线性发展方程的研究程序。已在SCI收录的国际学术期刊上发表论文300余篇，引用7000余篇次。主持国家自然科学基金面上项目4项，国家自然科学基金重点项目2项(第一参加人和项目负责人)、973项目1项(骨干科学家)、国家自然科学基金长江创新团队项目2项(PI)。

【前沿讲座三】

题目：Mix-training Physics-informed Neural Networks for the Rogue Waves of Nonlinear Schrödinger Equation

摘要：In this work, we propose Mix-training physics-informed neural networks (PINNs), a deep learning model with more approximation ability based on PINNs, combined with mixed training and prior information. We demonstrate the advantages of this model by exploring rogue waves with rich dynamic behavior in the nonlinear Schrödinger (NLS) equation. Numerical results show that compared with the original PINNs, this model can not only quickly recover the dynamical behavior of the rogue waves of NLS equation, but also significantly improve its approximation ability and absolute error accuracy, the prediction accuracy improved by two to three orders of magnitude. In particular, when the space-time domain of the solution expands or the solution has a local sharp region, the proposed model still has high prediction accuracy.

报告人简介

李彪，宁波大学云顶国际4008服务平台教授，博士生导师。主要从事非线性数学物理，孤立子与可积系统的研究。主持完成国家自然科学基金4项、省部级项目3项；参与完成国家自然科学基金重点项目2项；现主持国家自然科学基金面上项目1项。发表SCI论文100余篇，他引2000余次。

【联系人】

刘小川 教授 西安交通大学

Email：liuxiaochuan@mail.xjtu.edu.cn